

Интересная зависимость в распределении простых чисел.
При изучении последовательности всех простых чисел была обнаружена закономерность в их распределении. Закономерность выявлена при сопоставлении последовательных вычитаний в ряду простых чисел, из большего меньшего, и последующих вычитаний разностей.
Способ расчета следующий. Ряд всех простых чисел располагается по вертикали, от меньшего к большему. Разность соседних двух простых чисел записывается рядом с меньшим (верхним) числом, затем разности вычитаются в том же порядке, затем вторые разности вычитаются в том же порядке и т.д. В этом случае в горизонтальном ряду разностей можно отметить знакопеременный ряд чисел начинающихся как степени числа 2 и при указанном выше расположении отходящий от простого числа 5. Изучение полученного ряда показало, что он колеблется около значений 2х.
|
2 |
1 |
1 |
-1 |
3 |
-9 |
23 |
-53 |
115 |
-237 |
|
3 |
2 |
0 |
2 |
-6 |
14 |
-30 |
62 |
-122 |
220 |
|
5 |
2 |
2 |
-4 |
8 |
-16 |
32 |
-60 |
98 |
-124 |
|
7 |
4 |
-2 |
4 |
-8 |
16 |
-28 |
38 |
-26 |
-56 |
|
11 |
2 |
2 |
-4 |
8 |
-12 |
10 |
12 |
-82 |
248 |
|
13 |
4 |
-2 |
4 |
-4 |
-2 |
22 |
-70 |
166 |
-332 |
|
17 |
2 |
2 |
0 |
-6 |
20 |
-48 |
96 |
-166 |
252 |
|
19 |
4 |
2 |
-6 |
14 |
-28 |
48 |
-70 |
86 |
-86 |
|
23 |
6 |
-4 |
8 |
-14 |
20 |
-22 |
16 |
0 |
-28 |
|
29 |
2 |
4 |
-6 |
6 |
-2 |
-6 |
16 |
-28 |
56 |
|
31 |
6 |
-2 |
0 |
4 |
-8 |
10 |
-12 |
28 |
-98 |
|
37 |
4 |
-2 |
4 |
-4 |
2 |
-2 |
16 |
-70 |
210 |
|
41 |
2 |
2 |
0 |
-2 |
0 |
14 |
-54 |
140 |
-292 |
|
43 |
4 |
2 |
-2 |
-2 |
14 |
-40 |
86 |
-152 |
220 |
|
47 |
6 |
0 |
-4 |
12 |
-26 |
46 |
-66 |
68 |
-12 |
|
53 |
6 |
-4 |
8 |
-14 |
20 |
-20 |
2 |
56 |
-190 |
|
59 |
2 |
4 |
-6 |
6 |
0 |
-18 |
58 |
-134 |
258 |
|
61 |
6 |
-2 |
0 |
6 |
-18 |
40 |
-76 |
124 |
-168 |
|
67 |
4 |
-2 |
6 |
-12 |
22 |
-36 |
48 |
-44 |
4 |
|
71 |
2 |
4 |
-6 |
10 |
-14 |
12 |
4 |
-40 |
92 |
|
73 |
6 |
-2 |
4 |
-4 |
-2 |
16 |
-36 |
52 |
-38 |
Рис. 1. Начало таблицы расчетов.
График, построенный как зависимость порядкового номера простого числа (считая от второго значения) и логарифма по основанию 2 модулей полученных последовательных значений разности дает зависимость близкую к линейной с отдельными, непериодическими флуктуациями в сторону меньших значений.
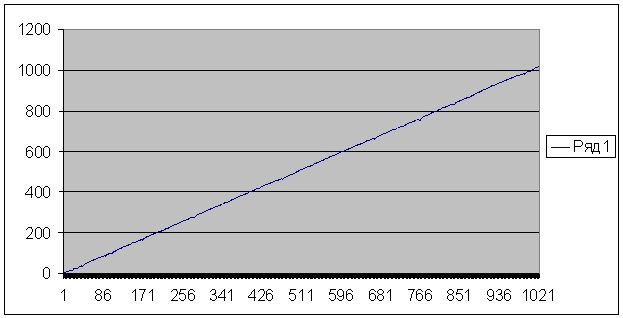 n
nРис.2. График зависимости порядкового номера числа от логарифма ряда разностей
Формула зависимости: Log2(x) = n , где x – модуль значения ряда
разностей начиная со второго, n – порядковый номер простого числа минус 4.
Расположение флуктуаций четко привязано к местам, где знак значений функции не изменяется на обратный. К сожалению рассчитать места флуктуаций пока не удалось. Но было обнаружено, что флуктуации повторяются во всех рядах с некоторым смещением.
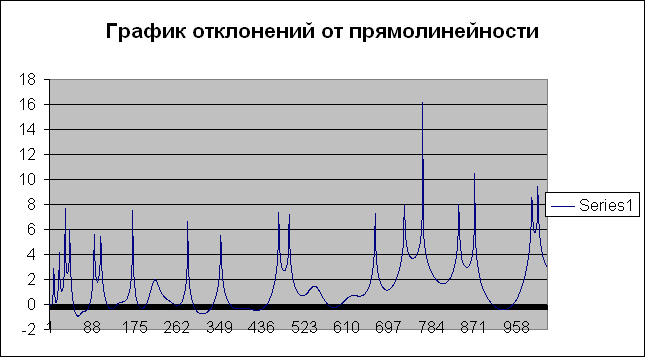 n
nМатематическое обоснование такой зависимости пока не проведено и проверка осуществлена всего лишь до 1022 значения (что связано с ресурсоемкостью расчетов).
Исходя из полученных данных, в перспективе возможно вычисление расположения любого простого числа в ряду натуральных чисел.
Моменты флуктуаций можно вычислить так как в рядах от чисел 2 и 5 разность моментов их возникновения равна 4. Кроме того, было обнаружено, что отношение логарифмов рядов от чисел 2 и 5 смещенные на 4 приблизительно вычисляются по формуле х/(х+4), где х - порядковый номер числа.
Не решены следующие проблемы:
1. Причина зависимости
2. Размер флуктуаций
Кипер Руслан Анатольевич
burewestnik@mail.ru
Дата первой публикации в сети Интернет - 23.01.2009